В этой статье мы расскажем о ключевых различиях между лабораторными и практическими работами в высшем образовании. Разберем цели, методы проведения и особенности организации каждого вида занятий. Объясним, как эти формы обучения помогают студентам развивать профессиональные навыки.

Определение лабораторных и практических работ

Лабораторные и практические работы — важные компоненты образовательного процесса в высших учебных заведениях. Они помогают студентам применить теоретические знания на практике и развить профессиональные навыки.

🤔 Определение

Лабораторная работа — это форма учебного занятия, при которой студенты под руководством преподавателя проводят эксперименты или опыты с использованием специального оборудования. Цель таких работ — проверка теоретических знаний и обучение методам экспериментального исследования.

🤔 Определение

Практическая работа — это вид учебной деятельности, направленный на формирование практических умений и навыков в конкретной профессиональной области. На таких занятиях студенты решают задачи, выполняют упражнения, анализируют ситуации, связанные с будущей профессией.

Хотя оба вида работ направлены на практическое применение знаний, между ними есть существенные различия в целях, методах проведения и организации.

Цели и задачи лабораторных работ

Лабораторные работы решают несколько важных образовательных задач:

• закрепление теоретических знаний на практике;

• развитие навыков работы с лабораторным оборудованием;

• формирование умений проводить научные эксперименты;

• обучение анализу и интерпретации полученных результатов.

Эффективность лабораторных работ подтверждается исследованиями. Например, согласно опросу, проведенному в 2023 году среди студентов технических вузов, 78% респондентов отметили, что лучше усваивают материал после проведения экспериментов.

Типичный ход лабораторной работы включает следующие этапы:

1. Подготовка к работе (изучение теории, инструктаж по технике безопасности).

2. Проведение эксперимента согласно методическим указаниям.

3. Обработка полученных данных.

4. Анализ результатов и формулирование выводов.

5. Оформление отчета о проделанной работе.

Цели и задачи практических работ

Практические работы направлены на достижение следующих целей:

• закрепление теоретического материала;

• развитие практических умений и навыков;

• формирование профессиональных компетенций;

• проверка уровня понимания изученного материала.

Примеры типичных заданий на практических работах для разных дисциплин:

• Экономика: расчет показателей эффективности предприятия.

• Юриспруденция: анализ правовых кейсов и составление документов.

• Программирование: написание кода для решения конкретных задач.

• Психология: проведение и интерпретация психологических тестов.

Структура практического занятия обычно включает:

1. Подготовку (повторение теории, ознакомление с заданием).

2. Выполнение практических заданий индивидуально или в группах.

3. Обсуждение результатов с преподавателем.

4. Подведение итогов и формулирование выводов.

Ключевые различия между лабораторными и практическими работами

Сравним лабораторные и практические работы по основным критериям:

1. Методика проведения:

   • Лабораторные работы: выполнение экспериментов, опытов.

   • Практические работы: решение задач, анализ ситуаций, выполнение проектов.

2. Используемое оборудование:

   • Лабораторные работы: специальное лабораторное оборудование, приборы.

   • Практические работы: обычно не требуют специального оборудования.

3. Форма отчетности:

   • Лабораторные работы: подробный отчет с описанием эксперимента и выводами.

   • Практические работы: выполненные задания, решения задач, презентации.

4. Влияние на итоговую оценку:

   • Лабораторные работы: обычно имеют больший вес в итоговой оценке.

   • Практические работы: чаще учитываются как текущая успеваемость.

5. Частота проведения:

   • Лабораторные работы: реже, из-за необходимости подготовки оборудования.

   • Практические работы: чаще, могут проводиться на каждом занятии.

Пример сравнения для курса по химии:

Особенности организации лабораторных работ

Организация лабораторных работ требует особого внимания к нескольким аспектам:

1. Требования к помещению и оборудованию:
   • Специально оборудованные лаборатории.
   • Наличие необходимых приборов и материалов.
   • Соблюдение норм безопасности (вентиляция, средства пожаротушения).
2. Роль преподавателя и лаборанта:
   • Преподаватель объясняет теорию, контролирует ход работы.
   • Лаборант готовит оборудование, следит за техникой безопасности.
3. Меры безопасности:
   • Проведение инструктажа перед каждой работой.
   • Использование средств индивидуальной защиты (очки, перчатки).
   • Строгое соблюдение правил работы с оборудованием и реактивами.
4. Типичная структура лабораторной работы:
   • Подготовка (10–15% времени).
   • Выполнение эксперимента (50–60% времени).
   • Обработка результатов (20–25% времени).
   • Оформление отчета и защита (10–15% времени).

Рекомендации по подготовке к лабораторным работам:

• Изучите теоретический материал заранее.
• Ознакомьтесь с методическими указаниями к работе.
• Подготовьте шаблон отчета до начала занятия.
• Повторите правила техники безопасности.

Особенности организации практических работ

Организация практических работ имеет свою специфику:

1. Формы проведения:

   • индивидуальные задания;

   • групповые проекты;

   • деловые игры и симуляции.

2. Виды заданий: 

   • решение профессиональных задач;

   • анализ кейсов из реальной практики;

   • разработка проектов;

   • проведение расчетов и анализа данных.

3. Роль преподавателя:

   • выступает как фасилитатор, направляя работу студентов;

   • предоставляет обратную связь и помощь при необходимости;

   • оценивает результаты работы.

4. Методы оценки результатов:

   • проверка правильности решения задач;

   • оценка качества анализа кейсов;

   • презентация и защита проектов;

   • тестирование практических навыков.

Инновационные подходы к проведению практических занятий:

• Использование компьютерных симуляторов (например, в медицинском образовании).

• Проведение виртуальных лабораторных работ (особенно актуально для дистанционного обучения).

• Применение технологий виртуальной и дополненной реальности.

Советы по эффективному участию в практических работах:

• Готовьтесь к занятиям, повторяя теорию.
• Активно участвуйте в обсуждениях и групповой работе.
• Не бойтесь задавать вопросы и просить пояснений.
• Старайтесь связывать полученные навыки с реальными профессиональными ситуациями.

Роль лабораторных и практических работ в формировании профессиональных компетенций

Лабораторные и практические работы играют ключевую роль в подготовке студентов к будущей профессиональной деятельности:

1. Связь с реальными производственными задачами:

   • Моделирование рабочих ситуаций.

   • Решение актуальных профессиональных проблем.

2. Развитие критического мышления и аналитических способностей:

   • Анализ данных и интерпретация результатов.

   • Принятие решений на основе полученной информации.

3. Формирование навыков командной работы:

   • Совместное выполнение проектов.

   • Распределение ролей и ответственности.

4. Подготовка к будущей профессиональной деятельности:

   • Освоение профессиональных инструментов и методик.

   • Формирование профессионального мышления.

Мнение экспертов: Согласно опросу работодателей, проведенному в 2023 году, 85% респондентов считают практический опыт, полученный в ходе обучения, ключевым фактором при найме молодых специалистов.

Статистика трудоустройства: Выпускники, активно участвовавшие в лабораторных и практических работах, находят работу по специальности в среднем на 30% быстрее, чем их сокурсники, пренебрегавшие этими формами обучения.

Современные тенденции в организации лабораторных и практических работ

Образовательные технологии постоянно развиваются, что отражается и на проведении лабораторных и практических работ:

1. Использование виртуальных лабораторий и симуляторов:

   • Возможность проводить эксперименты, недоступные в реальных условиях.

   • Безопасность при работе с опасными веществами или в экстремальных условиях.

2. Интеграция элементов дистанционного обучения:

   • Проведение онлайн-практикумов и вебинаров.

   • Использование платформ для совместной работы над проектами.

3. Применение проектного подхода:

   • Долгосрочные междисциплинарные проекты.

   • Решение реальных задач от компаний-партнеров.

4. Междисциплинарные лабораторные и практические работы:

   • Интеграция знаний из разных областей.

   • Развитие системного мышления.

Пример успешного внедрения: В 2023 году Технологический университет внедрил систему виртуальных лабораторий для студентов инженерных специальностей. Это позволило увеличить количество выполняемых работ на 40% без дополнительных затрат на оборудование.

Перспективы развития:

• Использование искусственного интеллекта для персонализации практических заданий.
• Внедрение технологий блокчейн для верификации полученных навыков.
• Расширение сотрудничества с индустрией для создания актуальных практических кейсов.

Заключение: Выбор между лабораторной и практической работой

Выбор между лабораторной и практической работой зависит от нескольких факторов:

• Цели обучения: что важнее — освоение экспериментальных методов или решение практических задач?

• Специфика дисциплины: некоторые предметы требуют больше лабораторных экспериментов, другие — практических упражнений.

• Доступные ресурсы: наличие необходимого оборудования и материалов.

• Уровень подготовки студентов: более сложные лабораторные работы могут требовать предварительного освоения базовых навыков на практических занятиях.

Важность баланса: Оптимальное сочетание лабораторных и практических работ обеспечивает комплексное формирование профессиональных компетенций студентов. Это позволяет выпускникам быть более конкурентоспособными на рынке труда.

Помните, что практический опыт, получаемый в ходе лабораторных и практических работ, — это ваше преимущество при трудоустройстве. Относитесь к этим занятиям серьезно и старайтесь извлечь максимум пользы из каждого из них. Активное участие в лабораторных и практических работах поможет вам:

• развить критическое мышление;
• научиться применять теорию на практике;
• освоить профессиональные инструменты;
• сформировать навыки командной работы.

Часто задаваемые вопросы

Чем отличается зачет от экзамена: ключевые различия

В учебном процессе зачет и экзамен являются важными формами контроля знаний, однако у них есть ряд ключевых отличий. Понимание этих различий поможет студентам лучше подготовиться к каждому из этих испытаний.

• Цель

Основная цель зачета — оценить степень усвоения материала и готовность студента к дальнейшему изучению дисциплины. Он служит своего рода промежуточной проверкой знаний.

Экзамен нацелен на глубокую оценку знаний и умений студента по предмету. Он часто подводит итоги изучения курса и повлияет на итоговую оценку за семестр или год.

• Формат

Зачет проводится в различных форматах, включая устное, письменное или тестирование. Обычно он включает в себя простые вопросы и задания, которые проверяют базовые знания.

Экзамен, как правило, имеет строгий формат. Он включает как теоретические вопросы, так и практические задания, требующие глубокого анализа и применения знаний.

• Уровень сложности

Зачеты, как правило, имеют меньший уровень сложности. Студентам предлагаются вопросы, охватывающие основные аспекты изученного материала, что позволяет им продемонстрировать общее понимание предмета.

Экзамены обычно имеют высокий уровень сложности. Они включают вопросы, требующие критического мышления, анализа и синтеза информации.

• Последствия

Успешное прохождение зачета, как правило, позволяет студенту перейти к следующему этапу обучения по данной дисциплине. Негативный результат, хотя и требует пересдачи, не оказывает столь серьезного влияния на итоговую оценку.

Результаты экзамена существенно повлияют на итоговую оценку за курс. Негативный результат потребует дополнительных усилий, таких как пересдача экзамена или выполнение дополнительных заданий.

• Система оценки

У зачета только две формы оценки — «зачтено» или «незачтено». Без определенных цифр и отметок.

Экзамен же оценивается традиционным способом: студенту ставят «неуд», «удовлетворительно», «хорошо» и «отлично».

Правила подготовки к зачету и экзамену – в чем различия

Подготовка к зачету и экзамену требует разных подходов и стратегий, что связано с различиями в цели, формате и уровне сложности этих мероприятий. Рассмотрим основные отличия в подготовке к зачету и экзамену.

Подготовка к зачету обычно требует повторения и закрепления основных тем курса. Студентам необходимо изучить ключевые понятия, определения и основные принципы. Подготовка к экзамену требует глубокого изучения материала, включая дополнительные источники и литературу. Здесь важно не только знание фактов, но и умение анализировать, сравнивать и применять теоретические знания на практике.

Подготовка к зачету, как правило, занимает меньше времени. Студенты эффективно готовятся за несколько дней, особенно если уже знакомы с материалом. Основное внимание стоит уделить повторению и систематизации знаний.

Подготовка к экзамену требует длительного времени, поэтому важно начать ее заранее. Рекомендуется разработать график подготовки, который включает в себя не только изучение материала, но и время на практику и тестирование.

Если «завалил» – что делать дальше? Можно ли пересдать экзамен и зачет

Неудача на зачетах и экзаменах — ситуация, с которой сталкиваются многие студенты. Важно помнить, что такие моменты не являются концом света, и существует ряд шагов, которые предпринимают для улучшения ситуации.

Прежде всего, стоит трезво оценить произошедшее. Постарайтесь понять, почему вы не справились с экзаменом или зачетом. Возможные причины включают:

• недостаточная подготовка;
• стресс или волнение в день экзамена;
• непонимание заданий или вопросов.

Каждое учебное заведение имеет правила относительно пересдачи зачетов и экзаменов. Обычно информация о пересдачах размещена в учебных планах, на стенде с расписанием или на сайте вуза. Поэтому, если вы не знаете или пропустили момент, когда оговаривалась дата пересдачи, обязательно позвоните на кафедру или преподавателю и уточните эту информацию.

После этого уже составляйте план подготовки.

При подготовке используйте дополнительные источники, такие как книги, онлайн-курсы и видеолекциии, а также старые задания и тесты для практики. Это поможет привыкнуть к формату вопросов.

Не забывайте о важности психологической подготовки. После неудачи возникает чувство неуверенности. Используйте техники релаксации, такие как медитация или физическая активность. Постепенно увеличивайте сложность задач, чтобы восстановить уверенность в силах.

Неудачи на зачетах и экзаменах — это часть учебного процесса.

Главное — правильно оценить ситуацию, понять причины и разработать план действий. Многие вузы предлагают возможность пересдачи, что дает шанс улучшить знания и навыки. Главное — не терять веру в себя и продолжать учиться.

Методы решения уравнений и неравенств

Решение уравнений и неравенств — это одна из центральных тем в высшей математике. Эти задачи требуют применения различных методов, в зависимости от типа уравнения или неравенства и условий, при которых они решаются. В этом разделе мы рассмотрим основные методы, которые помогут эффективно решать уравнения и неравенства.

Линейные уравнения и неравенства имеют вид ax+b=0 или ax+b≥0, где a и b — константы. Для их решения используются следующие методы:

• Алгебраический метод

Для линейного уравнения ax+b=0 переменная x выражается через известные коэффициенты:

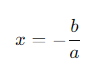
Линейные неравенства решаются путем изолирования переменной x, как в уравнении, с учетом направления знака неравенства. Если уравнение умножается или делится на отрицательное число, знак неравенства меняется на противоположный.

• Графический метод

Для уравнений типа ax+b=0 можно построить график линейной функции y=ax+b и определить точку пересечения с осью абсцисс (x-ось). Решение уравнения соответствует абсциссе этой точки. В случае неравенств анализируется, на каком интервале график лежит выше или ниже оси абсцисс.

Квадратные уравнения имеют вид ax+bx+c=0, где a≠0. Основные методы их решения:

• Формула дискриминанта

Для квадратного уравнения вычисляется дискриминант D:

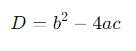
В зависимости от значения дискриминанта определяются корни уравнения.

1. Если D>0, уравнение имеет два различных корня.
2. Если D=0, уравнение имеет один корень (двойной).
3. Если D<0, уравнение не имеет вещественных решений.

Квадратное уравнение можно решить путем разложения многочлена на множители:

Затем находятся корни x1​ и x2​ уравнения.

Показательные уравнения имеют вид а^х = b, а логарифмические уравнения log_a(x)=b

Применение логарифмов позволяет выразить переменную x. Например:

Важно учитывать область допустимых значений для логарифмических уравнений: подлогарифмическое выражение должно быть положительным.

Иррациональные уравнения содержат переменную под знаком корня, например:

Для избавления от корня обе части уравнения возводятся в квадрат (или другую степень), после чего решается полученное алгебраическое уравнение:

После возведения в степень важно проверять полученные корни на наличие посторонних решений, которые могли возникнуть в процессе возведения.

Тригонометрические уравнения содержат тригонометрические функции (например, sin⁡(x)=a. Для их решения применяются:

• Метод приведения к основным тригонометрическим функциям: если уравнение содержит сложные выражения, их можно преобразовать с помощью тригонометрических тождеств, таких как формулы сложения или двойных углов.
• Использование тригонометрического круга: равнения типа sin⁡(x)=a решаются с помощью тригонометрического круга, который позволяет найти все возможные значения x на интервале от 0 до 2π.

Как справиться с трудностями при решении задач

Решение задач по высшей математике может быть сложным процессом, особенно если вы сталкиваетесь с непривычными или сложными темами. Однако трудности можно преодолеть, если применять правильные подходы и методики. В этом разделе мы рассмотрим стратегии, которые помогут справиться с проблемами и повысить эффективность при решении математических задач.

• Разбейте задачу на части

Одна из распространенных трудностей — объемная или сложная структура задачи. Чтобы упростить процесс решения, попробуйте разбить задачу на несколько более простых шагов.

1. Внимательно прочитайте задачу и выделите все ключевые моменты и данные. Определите, что именно нужно найти или доказать.
2. Если задача многослойная, постарайтесь решить ее частями. Найдите промежуточные результаты, которые приведут вас к конечному решению.
3. Подумайте, какие методы и формулы будут наиболее эффективны для решения каждой части задачи.

• Используйте аналогии

Если вы сталкиваетесь с новой задачей, которая кажется сложной, попробуйте найти аналогии с уже решенными задачами. Это поможет вам лучше понять структуру и подходы к решению. Вспомните задачи, которые вы уже решали, и подумайте, как их решения можно применить к текущей задаче. Некоторые из них решаются по шаблонам, особенно если они относятся к типовым математическим проблемам (например, уравнения или неравенства).

• Изучите теоретические основы

Иногда трудности возникают из-за недостаточного понимания теории. Если вам сложно решить задачу, важно вернуться к изучению теоретических основ: пересмотрите формулы, теоремы и правила, которые могут быть применимы к данной задаче. Убедитесь, что вы правильно их понимаете и умеете применять.

Изучение примеров с подробными решениями помогает лучше понять, как применять теоретические знания на практике.

• Используйте графический подход

Многие задачи можно упростить с помощью визуализации. В задачах с функциями, уравнениями или неравенствами постройте график, чтобы лучше понять, как ведет себя функция и где находятся ее корни. Если задача включает в себя геометрические или пространственные компоненты, нарисуйте схему или диаграмму, чтобы упростить понимание.

• Попробуйте несколько подходов

Не всегда первый метод решения задачи оказывается правильным или эффективным. Если вам не удается найти решение, попробуйте другие методы. Если один подход не дал результата, попробуйте применить другой метод (например, графический, алгебраический или числовой). Иногда переформулирование задачи или представление ее в другом виде (например, с использованием других переменных или формул) может облегчить решение.

• Не бойтесь ошибок

Ошибки — это часть процесса обучения, особенно при решении сложных задач. Не бойтесь допускать ошибки и использовать их как возможность для обучения. Даже если вы уверены в своем решении, проверьте все шаги и расчеты на наличие арифметических ошибок. Если решение оказалось неверным, разберите его и постарайтесь понять, где была допущена ошибка. Это поможет вам избежать подобных ошибок в будущем.

• Обратитесь за помощью

Если задача кажется слишком сложной или непонятной, не стесняйтесь обратиться за помощью. Преподаватели могут помочь вам разобраться в сложных вопросах и предложить пути решения. Существуют онлайн-курсы, видеоролики и статьи, которые могут помочь вам лучше понять тему и найти подход к решению.

• Регулярная практика

Математика требует регулярной практики для развития навыков и повышения уверенности. Постоянное решение задач помогает лучше понять логику и методы решения. Практикуйтесь на простых задачах, чтобы укрепить основы, и постепенно переходите к более сложным. Учебники и сборники задач предоставляют много вариантов для самостоятельной практики, что помогает закрепить изученные темы.

Разбираем типичные ошибки в задачах по высшей математике

Решение задач по высшей математике требует внимания к деталям и хорошего понимания теории. Даже опытные студенты иногда допускают ошибки, которые могут серьезно повлиять на результат. В этом разделе мы рассмотрим наиболее распространенные ошибки, встречающиеся при решении задач по высшей математике, и предложим советы, как их избежать.

• Неправильное понимание условий задачи

Часто студенты начинают решать задачу, не полностью разобравшись в ее условиях. Внимательно читайте условия задачи несколько раз, прежде чем приступать к решению. Определите, что конкретно требуется найти или доказать, и составьте план действий. Если какие-то условия кажутся неоднозначными, переформулируйте их в более понятной форме.

• Пренебрежение областью допустимых значений (ОДЗ)

Одной из самых распространенных ошибок является игнорирование области допустимых значений (ОДЗ), особенно в задачах с дробями, корнями или логарифмами. Это может привести к некорректным результатам.

В первую очередь анализируйте ОДЗ для каждой задачи. Например, при решении логарифмических уравнений всегда проверяйте, что подлогарифмическое выражение положительно, а при работе с дробями — что знаменатель не равен нулю.

• Ошибки в использовании математических формул

Некорректное применение или запоминание формул также является распространенной ошибкой. В результате этого решение может стать неверным уже на первых шагах.

Перед применением любой формулы убедитесь, что вы помните ее правильно и понимаете, в каком контексте она работает. При необходимости держите под рукой справочные материалы или таблицы формул.

• Ошибки при работе с знаками

Работа со знаками в алгебраических выражениях, особенно при раскрытии скобок или решении уравнений и неравенств, часто вызывает затруднения.

Будьте особенно внимательны при работе со знаками, особенно в сложных выражениях. Перепроверяйте раскрытие скобок и выполнение арифметических операций, чтобы избежать лишних ошибок.

• Неправильное использование тригонометрических тождеств

Тригонометрические задачи могут вызвать трудности из-за множества тождеств, которые необходимо применять для упрощения выражений.

Прежде чем приступать к решению, убедитесь, что вы выбрали правильное тождество для упрощения выражения. Используйте таблицу тригонометрических формул, чтобы исключить ошибки.

• Ошибки в расчетах

Даже при правильном понимании задачи и верном использовании методов часто случаются ошибки в арифметических вычислениях. Это может существенно повлиять на конечный результат.

Перепроверяйте свои расчеты на каждом этапе решения. Иногда полезно выполнить обратную проверку результата, чтобы убедиться в его правильности.

• Пропуск промежуточных шагов

Стремясь ускорить процесс решения, многие студенты пропускают промежуточные шаги и сразу переходят к заключительным действиям, что увеличивает вероятность ошибок.

Никогда не пропускайте важные шаги в решении задачи, даже если они кажутся очевидными. Ведение подробных записей поможет вам легче находить и исправлять ошибки.

Алгоритм решения даже самой сложной задачи

При решении сложных задач по высшей математике важно не только иметь хорошие теоретические знания, но и выработать четкий пошаговый алгоритм, который поможет избежать ошибок и эффективно двигаться к решению. Такой алгоритм можно применять к задачам любой сложности — от простых уравнений до сложных интегралов и дифференциальных уравнений. В этом разделе представлен универсальный алгоритм, который можно использовать для решения даже самых трудных задач.

• Внимательно прочитайте и проанализируйте условие задачи

Определите, что является искомым в задаче — неизвестная величина, функция или доказательство. Внимательно выпишите все известные параметры, условия и ограничения, данные в задаче. Постарайтесь понять, как все элементы задачи взаимосвязаны и какие математические зависимости могут быть использованы.

• Определите область допустимых значений (ОДЗ)

Перед началом решения важно определить область допустимых значений переменных, чтобы избежать ошибок и неработающих решений. Если задача включает дроби, корни, логарифмы или тригонометрические функции, важно сразу найти ограничения на переменные, при которых эти выражения имеют смысл.

• Выберите подходящие методы и инструменты

Для решения сложных задач необходимо выбрать правильные методы. Основная сложность часто заключается в том, чтобы найти наиболее эффективный подход.

1. Алгебраические методы: используйте, если задача связана с уравнениями и преобразованиями.
2. Графические методы: построение графиков помогает визуализировать решение и понять поведение функции.
3. Аналитические методы: подходят для решения дифференциальных и интегральных уравнений, анализа функций и нахождения пределов.
4. Численные методы: если задача не имеет точного аналитического решения, можно использовать численные подходы, такие как метод Ньютона или симплекс-метод.

• Разбейте задачу на несколько этапов

Решение сложной задачи часто состоит из нескольких взаимосвязанных шагов. Вместо того чтобы пытаться решить ее сразу целиком, полезно разделить задачу на несколько более простых частей.

1. Решите промежуточные подзадачи: найдите решения для каждой части задачи по отдельности.
2. Используйте результаты на каждом этапе: применяйте найденные решения для перехода к следующему этапу.

• Решайте пошагово, следуя логике

Записывайте все промежуточные шаги: Это поможет не потерять нить рассуждений и проще выявить ошибки, если что-то пойдет не так. Проверяйте свои действия на каждом этапе: После выполнения каждого шага проверяйте, не противоречат ли ваши действия условиям задачи.

• Используйте проверенные методы

После нахождения решения не торопитесь с выводами — обязательно проверьте правильность полученного результата.

1. Подставьте найденное значение в исходное выражение: это поможет проверить, соответствует ли результат условиям задачи.
2. Используйте альтернативные методы: иногда задача допускает решение несколькими способами. Если возможно, попробуйте решить ее другим методом и сравните результаты.
3. Проверка граничных случаев: если задача содержит параметры или переменные, проверьте решение для граничных значений этих параметров. Это поможет убедиться, что решение устойчиво.

• Оформите решение и сделайте выводы

Запишите итоговый ответ. Если задача требовала найти конкретное значение или доказать утверждение, четко запишите окончательный ответ. Объясните кратко логику вашего решения и обоснованность результата.

Примеры решений задач по высшей математике

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT