В этой статье мы расскажем, как правильно оформлять ссылки на интернет-источники в научных работах. Разберем требования ГОСТа, рассмотрим примеры для разных типов ресурсов и поделимся полезными инструментами для автоматизации процесса.

Что такое ссылка на интернет-ресурс и зачем ее правильно оформлять

Ссылка на интернет-ресурс — это библиографическое описание электронного документа, размещенного в сети Интернет. Правильное оформление таких ссылок — не просто формальность, а важная часть любой научной или учебной работы.

Зачем это нужно? Давайте разберемся:

• Подтверждает достоверность информации. Читатель может проверить источник и убедиться в надежности данных.
• Демонстрирует академическую честность. Вы показываете, что уважаете труд других исследователей.
• Помогает избежать плагиата. Четкое указание источников защищает вас от обвинений в присвоении чужих идей.
• Облегчает поиск информации. Другие исследователи смогут легко найти использованные вами материалы.

✏ Заметка По данным исследования, проведенного в 2023 году, более 80% студентов регулярно используют интернет-источники при написании работ. При этом только 60% знают, как правильно оформить на них ссылки.

Основные правила оформления ссылок на интернет-ресурсы по ГОСТ Р 7.0.5-2008

ГОСТ Р 7.0.5-2008 — это государственный стандарт, который регламентирует правила оформления библиографических ссылок. Он вступил в силу 1 января 2009 года и с тех пор является основным руководством при оформлении научных работ в России.

Ключевые требования стандарта к оформлению ссылок на электронные ресурсы:

1. Указание автора (если есть).
2. Название веб-страницы или документа.
3. Тип ресурса [Электронный ресурс].
4. Полный URL-адрес.
5. Дата обращения.

✏ Заметка

Указание даты обращения обязательно. Почему? Содержание веб-страниц может меняться, и дата позволяет понять, какую версию информации вы использовали.

Структура библиографической ссылки на интернет-ресурс

Разберем каждый элемент подробнее:

1. Автор. Указывается, если известен. Формат: Фамилия И.О. Пример: Иванов А.А.
2. Название. Приводится полностью, без сокращений. Пример: «Методы исследования в психологии».
3. Тип документа. Всегда указывается в квадратных скобках. Пример: [Электронный ресурс].
4. URL. Полный адрес страницы. Пример: URL: https://www.example.com/article.
5. Дата обращения. Указывается в круглых скобках. Пример: (дата обращения: 01.07.2024).

📖 Пример полной ссылки

Иванов А.А. Методы исследования в психологии [Электронный ресурс]. URL: https://www.example.com/article (дата обращения: 01.07.2024).

Особенности оформления ссылок на разные типы интернет-ресурсов

Разные типы интернет-ресурсов требуют немного разного подхода к оформлению. Рассмотрим основные варианты:

1. Статьи из электронных журналов: Автор А.А. Название статьи // Название журнала. Год. № X. URL: http://www.example.com/article (дата обращения: ДД.ММ.ГГГГ).
2. Веб-сайты: Название сайта [Электронный ресурс]. URL: http://www.example.com (дата обращения: ДД.ММ.ГГГГ).
3. Блоги: Автор А.А. Название записи [Электронный ресурс] // Название блога. Дата публикации. URL: http://www.example.com/blog-post (дата обращения: ДД.ММ.ГГГГ).
4. Социальные сети: Автор А.А. Текст поста [Электронный ресурс] // Название соц. сети. Дата публикации. URL: http://www.example.com/post (дата обращения: ДД.ММ.ГГГГ).
5. Видео с YouTube: Автор А.А. Название видео [Электронный ресурс] // YouTube. Дата публикации. URL: http://www.youtube.com/watch?v=xxxxx (дата обращения: ДД.ММ.ГГГГ).
6. Электронные книги: Автор А.А. Название книги [Электронный ресурс]. Место издания: Издательство, год. URL: http://www.example.com/book (дата обращения: ДД.ММ.ГГГГ).

Пошаговая инструкция по оформлению ссылки на интернет-ресурс

Давайте разберем процесс оформления ссылки шаг за шагом:

1. Определите тип ресурса (статья, веб-сайт, видео и т.д.).

2. Найдите всю необходимую информацию:

   • имя автора (если есть);

   • точное название страницы или документа;

   • дата публикации (если указана);

   • полный URL-адрес.

3. Запишите дату, когда вы обращались к ресурсу.

4. Составьте ссылку, располагая элементы в правильном порядке.

5. Проверьте, все ли элементы на месте и правильно ли они оформлены.

💡 Совет

Создайте для себя шаблон оформления ссылок для каждого типа ресурсов. Это сэкономит время при работе с большим количеством источников.

Типичные ошибки при оформлении ссылок на интернет-ресурсы

Давайте разберем самые распространенные ошибки и как их избежать:

• Неполный URL. Всегда копируйте полный адрес страницы, включая «https://».
• Отсутствие даты обращения. Это обязательный элемент для интернет-источников.
• Неправильный порядок элементов. Следуйте структуре, описанной в ГОСТе.
• Использование устаревших стандартов. Убедитесь, что вы используете актуальную версию ГОСТа.

Инструменты для автоматического оформления ссылок

Существуют удобные инструменты, которые могут значительно облегчить процесс оформления библиографии:

1. Mendeley. Бесплатная программа для управления библиографией и научными статьями.
2. Zotero. Открытое программное обеспечение для сбора и организации источников.
3. Citethisforme. Онлайн-инструмент для быстрого создания ссылок.

Как они работают? Вы вводите URL или информацию об источнике, а программа автоматически формирует ссылку в нужном формате.

✏ Заметка Даже используя автоматические инструменты, всегда проверяйте результат. Иногда программы могут ошибаться или не учитывать специфические требования вашего учебного заведения.

Примеры правильно оформленных ссылок на различные интернет-ресурсы

Давайте рассмотрим несколько конкретных примеров:

1. Статья с сайта: Иванов И.И. Влияние социальных сетей на успеваемость студентов [Электронный ресурс] // Образование и наука. 2024. URL: https://www.edu-science.ru/articles/123 (дата обращения: 04.07.2024).
2. Электронный журнал: Петров П.П. Новые методы дистанционного обучения // Педагогика онлайн. 2023. № 5. URL: https://www.ped-online.ru/article/2023/5/3 (дата обращения: 04.07.2024).
3. Видео на YouTube: Образовательный канал «Знание». Как написать дипломную работу [Электронный ресурс] // YouTube. 15.03.2024. URL: https://www.youtube.com/watch?v=abcdefgh (дата обращения: 04.07.2024).
4. Пост в социальной сети: Сидоров С.С. О важности правильного оформления ссылок [Электронный ресурс] // Facebook. 01.06.2024. URL: https://www.facebook.com/sidorov/posts/123456789 (дата обращения: 04.07.2024).

Как оформлять ссылки на интернет-ресурсы в тексте работы

Существует три основных способа оформления ссылок в тексте:

1. Внутритекстовые ссылки. Приводятся непосредственно в тексте в круглых скобках. Пример: «Согласно последним исследованиям (Иванов И.И. Влияние социальных сетей на успеваемость студентов. URL: https://www.edu-science.ru/articles/123)...»
2. Подстрочные ссылки. Нумеруются и приводятся внизу страницы. Пример в тексте: «Как отмечает Петров П.П.¹...» Внизу страницы: «¹ Петров П.П. Новые методы дистанционного обучения // Педагогика онлайн. 2023. № 5. URL: https://www.ped-online.ru/article/2023/5/3 (дата обращения: 04.07.2024).»
3. Затекстовые ссылки. Нумеруются и приводятся в конце работы в списке литературы. Пример в тексте: «Исследования показывают [1]...» В списке литературы: «1. Иванов И.И. Влияние социальных сетей на успеваемость студентов [Электронный ресурс] // Образование и наука. 2024. URL: https://www.edu-science.ru/articles/123 (дата обращения: 04.07.2024).»

Важно: Уточните у вашего научного руководителя, какой тип ссылок предпочтителен для вашей работы.

Заключение: важность соблюдения стандартов при оформлении ссылок

Правильное оформление ссылок на интернет-ресурсы — не просто формальность, а важный элемент академической культуры. Это показатель вашего профессионализма и уважения к научному сообществу.

Помните:

• Стандарты могут меняться. Всегда проверяйте актуальность используемого ГОСТа.
• Разные учебные заведения могут иметь свои дополнительные требования. Уточняйте их у научного руководителя.
• Практика — ключ к успеху. Чем больше вы работаете с источниками, тем легче становится их правильно оформлять.

💡 Совет Создайте для себя краткую шпаргалку с основными правилами оформления ссылок и держите ее под рукой при работе над научными текстами.

Часто задаваемые вопросы

1. Нужно ли указывать дату обращения для всех интернет-источников? Да, дата обращения — обязательный элемент для всех ссылок на интернет-ресурсы по ГОСТ Р 7.0.5-2008.

2. Как оформить ссылку, если автор не указан? В этом случае ссылка начинается с названия материала.

3. Можно ли сокращать длинные URL-адреса? По ГОСТу сокращать URL не рекомендуется. Однако, если адрес очень длинный, уточните у научного руководителя возможность использования сервисов для сокращения ссылок.

4. Как оформить ссылку на сайт в целом, а не на конкретную страницу? Указывайте название сайта, URL главной страницы и дату обращения.

5. Нужно ли указывать номер страницы для интернет-источников? Для интернет-источников номер страницы обычно не указывается, так как веб-страницы часто не имеют фиксированной пагинации.

6. Как оформить ссылку на PDF-документ, скачанный с сайта? Оформляйте так же, как и обычную веб-страницу, но добавьте информацию о формате файла. Например: Автор А.А. Название документа [Электронный ресурс]: PDF-документ. URL: http://www.example.com/document.pdf (дата обращения: 04.07.2024).

7. Нужно ли использовать кавычки в названии интернет-ресурса? Да, название интернет-ресурса заключается в кавычки-«ёлочки». Например: «Научная электронная библиотека» [Электронный ресурс]. URL: https://www.elibrary.ru (дата обращения: 04.07.2024).

8. Как оформить ссылку на статью из электронной энциклопедии? Пример оформления: Название статьи // Название энциклопедии [Электронный ресурс]. Дата публикации или последнего обновления (если указана). URL: http://www.example.com/article (дата обращения: 04.07.2024).

9. Что делать, если интернет-ресурс на иностранном языке? Оформляйте ссылку на языке оригинала. Если в работе используется кириллица, можно дать перевод названия в квадратных скобках после оригинального названия.

10. Как правильно указывать дату обращения — словами или цифрами? По ГОСТ Р 7.0.5-2008 дата обращения указывается цифрами в формате: (дата обращения: ДД.ММ.ГГГГ).

Методы решения уравнений и неравенств

Решение уравнений и неравенств — это одна из центральных тем в высшей математике. Эти задачи требуют применения различных методов, в зависимости от типа уравнения или неравенства и условий, при которых они решаются. В этом разделе мы рассмотрим основные методы, которые помогут эффективно решать уравнения и неравенства.

Линейные уравнения и неравенства имеют вид ax+b=0 или ax+b≥0, где a и b — константы. Для их решения используются следующие методы:

• Алгебраический метод

Для линейного уравнения ax+b=0 переменная x выражается через известные коэффициенты:

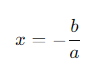
Линейные неравенства решаются путем изолирования переменной x, как в уравнении, с учетом направления знака неравенства. Если уравнение умножается или делится на отрицательное число, знак неравенства меняется на противоположный.

• Графический метод

Для уравнений типа ax+b=0 можно построить график линейной функции y=ax+b и определить точку пересечения с осью абсцисс (x-ось). Решение уравнения соответствует абсциссе этой точки. В случае неравенств анализируется, на каком интервале график лежит выше или ниже оси абсцисс.

Квадратные уравнения имеют вид ax+bx+c=0, где a≠0. Основные методы их решения:

• Формула дискриминанта

Для квадратного уравнения вычисляется дискриминант D:

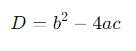
В зависимости от значения дискриминанта определяются корни уравнения.

1. Если D>0, уравнение имеет два различных корня.
2. Если D=0, уравнение имеет один корень (двойной).
3. Если D<0, уравнение не имеет вещественных решений.

Квадратное уравнение можно решить путем разложения многочлена на множители:

Затем находятся корни x1​ и x2​ уравнения.

Показательные уравнения имеют вид а^х = b, а логарифмические уравнения log_a(x)=b

Применение логарифмов позволяет выразить переменную x. Например:

Важно учитывать область допустимых значений для логарифмических уравнений: подлогарифмическое выражение должно быть положительным.

Иррациональные уравнения содержат переменную под знаком корня, например:

Для избавления от корня обе части уравнения возводятся в квадрат (или другую степень), после чего решается полученное алгебраическое уравнение:

После возведения в степень важно проверять полученные корни на наличие посторонних решений, которые могли возникнуть в процессе возведения.

Тригонометрические уравнения содержат тригонометрические функции (например, sin⁡(x)=a. Для их решения применяются:

• Метод приведения к основным тригонометрическим функциям: если уравнение содержит сложные выражения, их можно преобразовать с помощью тригонометрических тождеств, таких как формулы сложения или двойных углов.
• Использование тригонометрического круга: равнения типа sin⁡(x)=a решаются с помощью тригонометрического круга, который позволяет найти все возможные значения x на интервале от 0 до 2π.

Как справиться с трудностями при решении задач

Решение задач по высшей математике может быть сложным процессом, особенно если вы сталкиваетесь с непривычными или сложными темами. Однако трудности можно преодолеть, если применять правильные подходы и методики. В этом разделе мы рассмотрим стратегии, которые помогут справиться с проблемами и повысить эффективность при решении математических задач.

• Разбейте задачу на части

Одна из распространенных трудностей — объемная или сложная структура задачи. Чтобы упростить процесс решения, попробуйте разбить задачу на несколько более простых шагов.

1. Внимательно прочитайте задачу и выделите все ключевые моменты и данные. Определите, что именно нужно найти или доказать.
2. Если задача многослойная, постарайтесь решить ее частями. Найдите промежуточные результаты, которые приведут вас к конечному решению.
3. Подумайте, какие методы и формулы будут наиболее эффективны для решения каждой части задачи.

• Используйте аналогии

Если вы сталкиваетесь с новой задачей, которая кажется сложной, попробуйте найти аналогии с уже решенными задачами. Это поможет вам лучше понять структуру и подходы к решению. Вспомните задачи, которые вы уже решали, и подумайте, как их решения можно применить к текущей задаче. Некоторые из них решаются по шаблонам, особенно если они относятся к типовым математическим проблемам (например, уравнения или неравенства).

• Изучите теоретические основы

Иногда трудности возникают из-за недостаточного понимания теории. Если вам сложно решить задачу, важно вернуться к изучению теоретических основ: пересмотрите формулы, теоремы и правила, которые могут быть применимы к данной задаче. Убедитесь, что вы правильно их понимаете и умеете применять.

Изучение примеров с подробными решениями помогает лучше понять, как применять теоретические знания на практике.

• Используйте графический подход

Многие задачи можно упростить с помощью визуализации. В задачах с функциями, уравнениями или неравенствами постройте график, чтобы лучше понять, как ведет себя функция и где находятся ее корни. Если задача включает в себя геометрические или пространственные компоненты, нарисуйте схему или диаграмму, чтобы упростить понимание.

• Попробуйте несколько подходов

Не всегда первый метод решения задачи оказывается правильным или эффективным. Если вам не удается найти решение, попробуйте другие методы. Если один подход не дал результата, попробуйте применить другой метод (например, графический, алгебраический или числовой). Иногда переформулирование задачи или представление ее в другом виде (например, с использованием других переменных или формул) может облегчить решение.

• Не бойтесь ошибок

Ошибки — это часть процесса обучения, особенно при решении сложных задач. Не бойтесь допускать ошибки и использовать их как возможность для обучения. Даже если вы уверены в своем решении, проверьте все шаги и расчеты на наличие арифметических ошибок. Если решение оказалось неверным, разберите его и постарайтесь понять, где была допущена ошибка. Это поможет вам избежать подобных ошибок в будущем.

• Обратитесь за помощью

Если задача кажется слишком сложной или непонятной, не стесняйтесь обратиться за помощью. Преподаватели могут помочь вам разобраться в сложных вопросах и предложить пути решения. Существуют онлайн-курсы, видеоролики и статьи, которые могут помочь вам лучше понять тему и найти подход к решению.

• Регулярная практика

Математика требует регулярной практики для развития навыков и повышения уверенности. Постоянное решение задач помогает лучше понять логику и методы решения. Практикуйтесь на простых задачах, чтобы укрепить основы, и постепенно переходите к более сложным. Учебники и сборники задач предоставляют много вариантов для самостоятельной практики, что помогает закрепить изученные темы.

Разбираем типичные ошибки в задачах по высшей математике

Решение задач по высшей математике требует внимания к деталям и хорошего понимания теории. Даже опытные студенты иногда допускают ошибки, которые могут серьезно повлиять на результат. В этом разделе мы рассмотрим наиболее распространенные ошибки, встречающиеся при решении задач по высшей математике, и предложим советы, как их избежать.

• Неправильное понимание условий задачи

Часто студенты начинают решать задачу, не полностью разобравшись в ее условиях. Внимательно читайте условия задачи несколько раз, прежде чем приступать к решению. Определите, что конкретно требуется найти или доказать, и составьте план действий. Если какие-то условия кажутся неоднозначными, переформулируйте их в более понятной форме.

• Пренебрежение областью допустимых значений (ОДЗ)

Одной из самых распространенных ошибок является игнорирование области допустимых значений (ОДЗ), особенно в задачах с дробями, корнями или логарифмами. Это может привести к некорректным результатам.

В первую очередь анализируйте ОДЗ для каждой задачи. Например, при решении логарифмических уравнений всегда проверяйте, что подлогарифмическое выражение положительно, а при работе с дробями — что знаменатель не равен нулю.

• Ошибки в использовании математических формул

Некорректное применение или запоминание формул также является распространенной ошибкой. В результате этого решение может стать неверным уже на первых шагах.

Перед применением любой формулы убедитесь, что вы помните ее правильно и понимаете, в каком контексте она работает. При необходимости держите под рукой справочные материалы или таблицы формул.

• Ошибки при работе с знаками

Работа со знаками в алгебраических выражениях, особенно при раскрытии скобок или решении уравнений и неравенств, часто вызывает затруднения.

Будьте особенно внимательны при работе со знаками, особенно в сложных выражениях. Перепроверяйте раскрытие скобок и выполнение арифметических операций, чтобы избежать лишних ошибок.

• Неправильное использование тригонометрических тождеств

Тригонометрические задачи могут вызвать трудности из-за множества тождеств, которые необходимо применять для упрощения выражений.

Прежде чем приступать к решению, убедитесь, что вы выбрали правильное тождество для упрощения выражения. Используйте таблицу тригонометрических формул, чтобы исключить ошибки.

• Ошибки в расчетах

Даже при правильном понимании задачи и верном использовании методов часто случаются ошибки в арифметических вычислениях. Это может существенно повлиять на конечный результат.

Перепроверяйте свои расчеты на каждом этапе решения. Иногда полезно выполнить обратную проверку результата, чтобы убедиться в его правильности.

• Пропуск промежуточных шагов

Стремясь ускорить процесс решения, многие студенты пропускают промежуточные шаги и сразу переходят к заключительным действиям, что увеличивает вероятность ошибок.

Никогда не пропускайте важные шаги в решении задачи, даже если они кажутся очевидными. Ведение подробных записей поможет вам легче находить и исправлять ошибки.

Алгоритм решения даже самой сложной задачи

При решении сложных задач по высшей математике важно не только иметь хорошие теоретические знания, но и выработать четкий пошаговый алгоритм, который поможет избежать ошибок и эффективно двигаться к решению. Такой алгоритм можно применять к задачам любой сложности — от простых уравнений до сложных интегралов и дифференциальных уравнений. В этом разделе представлен универсальный алгоритм, который можно использовать для решения даже самых трудных задач.

• Внимательно прочитайте и проанализируйте условие задачи

Определите, что является искомым в задаче — неизвестная величина, функция или доказательство. Внимательно выпишите все известные параметры, условия и ограничения, данные в задаче. Постарайтесь понять, как все элементы задачи взаимосвязаны и какие математические зависимости могут быть использованы.

• Определите область допустимых значений (ОДЗ)

Перед началом решения важно определить область допустимых значений переменных, чтобы избежать ошибок и неработающих решений. Если задача включает дроби, корни, логарифмы или тригонометрические функции, важно сразу найти ограничения на переменные, при которых эти выражения имеют смысл.

• Выберите подходящие методы и инструменты

Для решения сложных задач необходимо выбрать правильные методы. Основная сложность часто заключается в том, чтобы найти наиболее эффективный подход.

1. Алгебраические методы: используйте, если задача связана с уравнениями и преобразованиями.
2. Графические методы: построение графиков помогает визуализировать решение и понять поведение функции.
3. Аналитические методы: подходят для решения дифференциальных и интегральных уравнений, анализа функций и нахождения пределов.
4. Численные методы: если задача не имеет точного аналитического решения, можно использовать численные подходы, такие как метод Ньютона или симплекс-метод.

• Разбейте задачу на несколько этапов

Решение сложной задачи часто состоит из нескольких взаимосвязанных шагов. Вместо того чтобы пытаться решить ее сразу целиком, полезно разделить задачу на несколько более простых частей.

1. Решите промежуточные подзадачи: найдите решения для каждой части задачи по отдельности.
2. Используйте результаты на каждом этапе: применяйте найденные решения для перехода к следующему этапу.

• Решайте пошагово, следуя логике

Записывайте все промежуточные шаги: Это поможет не потерять нить рассуждений и проще выявить ошибки, если что-то пойдет не так. Проверяйте свои действия на каждом этапе: После выполнения каждого шага проверяйте, не противоречат ли ваши действия условиям задачи.

• Используйте проверенные методы

После нахождения решения не торопитесь с выводами — обязательно проверьте правильность полученного результата.

1. Подставьте найденное значение в исходное выражение: это поможет проверить, соответствует ли результат условиям задачи.
2. Используйте альтернативные методы: иногда задача допускает решение несколькими способами. Если возможно, попробуйте решить ее другим методом и сравните результаты.
3. Проверка граничных случаев: если задача содержит параметры или переменные, проверьте решение для граничных значений этих параметров. Это поможет убедиться, что решение устойчиво.

• Оформите решение и сделайте выводы

Запишите итоговый ответ. Если задача требовала найти конкретное значение или доказать утверждение, четко запишите окончательный ответ. Объясните кратко логику вашего решения и обоснованность результата.

Примеры решений задач по высшей математике

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT

Фото: ChatGPT

В этой статье мы расскажем о лабораторном эксперименте в психологии — ключевом методе научного исследования. Разберем его особенности, этапы проведения и области применения. Дадим практические советы по планированию и реализации экспериментов.

Что такое лабораторный эксперимент в психологии и его значение

🤔 Определение

Лабораторный эксперимент в психологии — это метод исследования, при котором изучаемое явление воспроизводится в контролируемых условиях. Его главная цель — обеспечить воспроизводимость феномена при полном контроле исследуемых факторов.

Значение лабораторного эксперимента для психологии трудно переоценить:

1. Позволяет установить причинно-следственные связи.
2. Обеспечивает высокую точность измерений.
3. Дает возможность повторить исследование для проверки результатов.

По данным анализа научных публикаций, около 60% эмпирических исследований в психологии проводятся в форме лабораторных экспериментов. Это говорит о высокой востребованности метода в научном сообществе.

Основные характеристики и особенности лабораторного эксперимента

Лабораторный эксперимент отличается рядом ключевых особенностей:

• высокая степень контроля над переменными;
• искусственность условий;
• возможность точной регистрации данных;
• ограниченность в моделировании реальных жизненных ситуаций.

Независимые и зависимые переменные

В эксперименте выделяют два типа переменных:

1. Независимые — факторы, которыми манипулирует экспериментатор.

2. Зависимые — измеряемые реакции испытуемых.

Например, в исследовании влияния цвета на эмоциональное состояние:

• Независимая переменная — цвет окружения (красный, синий, зеленый).

• Зависимая переменная — уровень тревожности участников.

Преимущества и недостатки метода

Преимущества:

• высокая точность измерений;

• возможность установить причинно-следственные связи;

• контроль побочных переменных.

Недостатки:

• искусственность ситуации;

• ограниченная экологическая валидность;

• сложность изучения долгосрочных эффектов.

Важно понимать: лабораторный эксперимент — как микроскоп в биологии. Он позволяет детально изучить отдельные аспекты психики, но может упустить более широкую картину.

Этапы планирования и проведения лабораторного эксперимента

Формулировка гипотезы и определение переменных

На этом этапе исследователь:

• формулирует гипотезу;
• определяет независимые и зависимые переменные;
• операционализирует понятия (переводит их в измеряемые показатели).

📖 Пример

Гипотеза: «Прослушивание классической музыки улучшает кратковременную память». Независимая переменная: наличие/отсутствие классической музыки. Зависимая переменная: количество правильно воспроизведенных слов в тесте памяти.

Выбор экспериментального плана

Исследователь выбирает план эксперимента. Основные виды:

• межгрупповой (сравнение разных групп);

• внутригрупповой (одна группа в разных условиях);

• факторный (изучение влияния нескольких факторов).

Подбор участников и формирование выборки

На этом этапе определяется:

• размер выборки;

• критерии включения и исключения участников;

• метод формирования групп (случайный или уравнивание).

Подготовка оборудования и материалов

Исследователь:

• подбирает или разрабатывает методики измерения;

• готовит инструкции для участников;

• проводит пилотажное исследование для проверки процедуры.

Проведение эксперимента

Этот этап включает:

• инструктаж участников;

• предъявление стимулов и регистрацию реакций;

• контроль побочных переменных.

Анализ и интерпретация результатов

Заключительный этап:

• статистическая обработка данных;

• интерпретация результатов;

• формулировка выводов и их соотнесение с гипотезой.

Виды экспериментальных планов в лабораторных исследованиях

Простые (однофакторные) планы

Изучается влияние одной независимой переменной. Бывают:

• с контрольной группой;
• с предварительным и итоговым тестированием.

Пример: изучение влияния кофеина на скорость реакции.

Факторные планы

Исследуется влияние двух или более независимых переменных. Позволяют изучить:

• главные эффекты каждого фактора;

• эффекты взаимодействия факторов.

Пример: влияние типа задачи (вербальная/невербальная) и уровня шума (тишина/умеренный шум/сильный шум) на эффективность решения.

Многоуровневые планы

Независимая переменная имеет более двух уровней.

Пример: влияние дозировки препарата (низкая/средняя/высокая) на память.

Квазиэкспериментальные планы

Используются, когда полный контроль переменных невозможен. Основные виды:

• планы временных серий;

• планы ex-post-facto.

Выбор плана влияет на внутреннюю и внешнюю валидность исследования. Внутренняя валидность — степень, в которой изменения зависимой переменной можно приписать влиянию независимой. Внешняя валидность — возможность обобщения результатов на другие условия и выборки.

Методы контроля в лабораторном эксперименте

Метод прямого контроля

Суть: исследователь напрямую контролирует все известные побочные переменные.

Пример: в эксперименте по влиянию освещения на работоспособность контролируются температура, уровень шума, время суток.

Метод выравнивания условий

Все группы проходят эксперимент в одинаковых условиях, кроме воздействия независимой переменной.

Пример: при изучении влияния типа инструкции на выполнение задания все группы получают задания в одно время, в одинаковых помещениях, от одного экспериментатора.

Метод рандомизации

Случайное распределение участников по группам. Позволяет уравнять группы по неизвестным исследователю характеристикам.

По данным мета-анализов, рандомизация повышает надежность результатов на 15–20%.

Области применения лабораторного эксперимента в современной психологии

Лабораторный эксперимент широко применяется в различных областях психологии:

Пример: эксперименты Ж. Пиаже по изучению стадий развития интеллекта.

В некоторых областях, например, в клинической психологии, применение лабораторных экспериментов ограничено этическими соображениями и сложностью моделирования реальных ситуаций.

Этические аспекты проведения лабораторных экспериментов в психологии

Проведение психологических экспериментов требует строгого соблюдения этических норм:

Пример этической дилеммы — эксперимент Милгрэма по подчинению авторитету. Он вызвал споры о допустимости введения участников в заблуждение и создания стрессовых ситуаций.

Современные стандарты требуют одобрения экспериментов этическими комитетами. По данным опросов, около 95% психологов считают, что этические нормы в экспериментах стали строже за последние 30 лет.

Критика и ограничения лабораторного эксперимента в психологии

Несмотря на широкое применение, лабораторный эксперимент имеет ряд ограничений:

1. Проблема экологической валидности:

   • искусственность лабораторных условий;

   • сложность переноса результатов в реальную жизнь.

2. Ограниченность выборки:

   • частое использование студентов в качестве испытуемых;

   • проблема репрезентативности выборки.

3. Влияние экспериментатора на результаты:

   • эффект Розенталя (влияние ожиданий экспериментатора);

   • проблема двойного слепого метода в психологии.

4. Сложность изучения долгосрочных эффектов:

   • большинство экспериментов краткосрочны;

   • трудности в изучении развития и изменений во времени.

Исследователи пытаются преодолеть эти ограничения через:

• комбинирование лабораторных и полевых исследований;

• использование методов виртуальной реальности;

• проведение лонгитюдных исследований.

Альтернативные методы, такие как полевые эксперименты и естественные эксперименты, часто дополняют лабораторные исследования.

Будущее лабораторных экспериментов в психологии: тенденции и перспективы

Развитие технологий открывает новые возможности для лабораторных экспериментов:

1. Использование виртуальной и дополненной реальности:

   • создание более реалистичных экспериментальных условий;

   • изучение поведения в сложных социальных ситуациях.

2. Применение нейровизуализации:

   • интеграция психологических тестов с МРТ и ЭЭГ;

   • изучение нейронных коррелятов психических процессов.

3. Интеграция с методами big data и машинного обучения:

   • анализ больших объемов поведенческих данных;

   • создание более точных предсказательных моделей.

Пример инновационного исследования: использование VR для изучения социальных фобий, где участники взаимодействуют с виртуальными персонажами в различных социальных ситуациях.

Потенциальные этические проблемы включают:

• вопросы приватности при сборе больших объемов данных;

• риски психологического воздействия в VR-средах.

Эксперты прогнозируют, что в ближайшие 10–20 лет мы увидим:

• увеличение междисциплинарных исследований;

• рост использования мобильных технологий для сбора данных в реальном времени;

• развитие методов удаленного проведения экспериментов.

Заключение: значение лабораторных экспериментов для развития психологической науки

Лабораторные эксперименты остаются ключевым методом в психологии, позволяя:

• устанавливать причинно-следственные связи;

• проверять теоретические модели;

• разрабатывать новые методы диагностики и коррекции.

Основные преимущества метода:

• высокая степень контроля;

• возможность точных измерений;

• воспроизводимость результатов.

Ограничения:

• искусственность условий;

• сложность обобщения результатов;

• этические ограничения.

Важно понимать, что лабораторный эксперимент — не единственный метод психологического исследования. Для получения полной картины психологических явлений необходимо сочетание различных подходов:

• лабораторных и полевых экспериментов;

• наблюдений;

• опросов и интервью;

• анализа больших данных.

Критическое мышление и понимание методологии крайне важны для правильной интерпретации результатов психологических исследований. Студентам-психологам рекомендуется:

• внимательно изучать дизайн экспериментов;

• оценивать внутреннюю и внешнюю валидность исследований;

• рассматривать альтернативные объяснения полученных результатов.

В заключение отметим: несмотря на ограничения, лабораторный эксперимент остается «золотым стандартом» психологического исследования. Его развитие и совершенствование продолжает двигать вперед психологическую науку, открывая новые горизонты в понимании человеческой психики и поведения.

Часто задаваемые вопросы

1. Чем отличается лабораторный эксперимент от полевого? Лабораторный эксперимент проводится в контролируемых условиях, что позволяет изолировать изучаемые переменные. Полевой эксперимент проходит в естественной среде, обеспечивая большую экологическую валидность, но меньший контроль над переменными.

2. Какой размер выборки считается достаточным для лабораторного эксперимента? Размер выборки зависит от дизайна исследования и ожидаемого размера эффекта. Обычно рекомендуется минимум 30 участников на группу, но для более надежных результатов часто требуется больше.

3. Как решается проблема влияния эффекта Хоторна в лабораторных экспериментах? Эффект Хоторна (изменение поведения участников из-за осознания, что за ними наблюдают) минимизируется через:

   • использование слепого метода;

   • маскировку истинных целей эксперимента;

   • привыкание участников к экспериментальной обстановке.

4. Можно ли проводить лабораторные эксперименты онлайн? Да, с развитием технологий все больше экспериментов проводится онлайн. Это позволяет привлечь более разнообразную выборку, но требует особого внимания к контролю условий и обеспечению качества данных.

5. Как учитывается индивидуальная изменчивость в лабораторных экспериментах? Индивидуальная изменчивость учитывается через:

   • рандомизацию выборки;

   • использование внутригрупповых планов;

   • статистический контроль индивидуальных различий.

Помните, что понимание методологии лабораторных экспериментов — ключевой навык для студентов-психологов и исследователей. Это основа для критической оценки научной литературы и проведения собственных исследований.